一、归并排序
归并是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路。
归并过程为:比较a[i]和a[j]的大小,若a[i]≤a[j],则将第一个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1;否则将第二个有序表中的元素a[j]复制到r[k]中,并令j和k分别加上1,如此循环下去,直到其中一个有序表取完,然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现,先把待排序区间[s,t]以中点二分,接着把左边子区间排序,再把右边子区间排序,最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。
二、归并操作
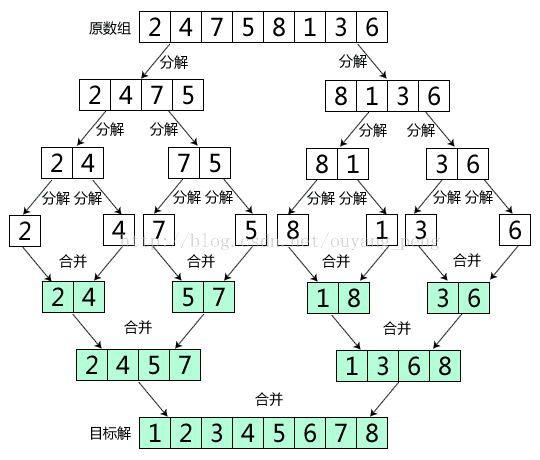
三、两路归并算法
1、算法基本思路 设两个有序的子文件(相当于输入堆)放在同一向量中相邻的位置上:R[low..m],R[m+1..high],先将它们合并到一个局部的暂存向量R1(相当于输出堆)中,待合并完成后将R1复制回R[low..high]中。(1)合并过程 合并过程中,设置i,j和p三个指针,其初值分别指向这三个记录区的起始位置。合并时依次比较R[i]和R[j]的关键字,取关键字较小的记录复制到R1[p]中,然后将被复制记录的指针i或j加1,以及指向复制位置的指针p加1。 重复这一过程直至两个输入的子文件有一个已全部复制完毕(不妨称其为空),此时将另一非空的子文件中剩余记录依次复制到R1中即可。(2)动态申请R1 实现时,R1是动态申请的,因为申请的空间可能很大,故须加入申请空间是否成功的处理。 2、归并算法
void Merge(SeqList R,int low,int m,int high) {//将两个有序的子文件R[low..m)和R[m+1..high]归并成一个有序的 //子文件R[low..high] int i=low,j=m+1,p=0; //置初始值 RecType *R1; //R1是局部向量,若p定义为此类型指针速度更快 R1=(ReeType *)malloc((high-low+1)*sizeof(RecType)); if(! R1) //申请空间失败 Error("Insufficient memory available!"); while(i<=m&&j<=high) //两子文件非空时取其小者输出到R1[p]上 R1[p++]=(R[i].key<=R[j].key)?R[i++]:R[j++]; while(i<=m) //若第1个子文件非空,则复制剩余记录到R1中 R1[p++]=R[i++]; while(j<=high) //若第2个子文件非空,则复制剩余记录到R1中 R1[p++]=R[j++]; for(p=0,i=low;i<=high;p++,i++) R[i]=R1[p];//归并完成后将结果复制回R[low..high] } //Merge 四、归并排序
归并排序有两种实现方法:自底向上和自顶向下。下面说说 自顶向下的方法
(1)分治法的三个步骤 设归并排序的当前区间是R[low..high],分治法的三个步骤是:①分解:将当前区间一分为二,即求分裂点 ②求解:递归地对两个子区间R[low..mid]和R[mid+1..high]进行归并排序;③组合:将已排序的两个子区间R[low..mid]和R[mid+1..high]归并为一个有序的区间R[low..high]。 递归的终结条件:子区间长度为1(一个记录自然有序)。 (2)具体算法 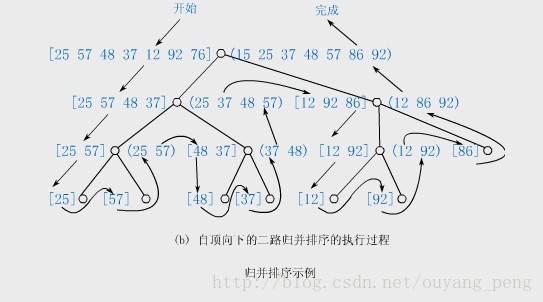
void MergeSortDC(SeqList R,int low,int high) {//用分治法对R[low..high]进行二路归并排序 int mid; if(low (3)算法MergeSortDC的执行过程 算法MergeSortDC的执行过程如下图所示的递归树。 
五、算法分析 1、稳定性 归并排序是一种稳定的排序。
2、存储结构要求 可用顺序存储结构。也易于在链表上实现。
3、时间复杂度 对长度为n的文件,需进行 趟二路归并,每趟归并的时间为O(n),故其时间复杂度无论是在最好情况下还是在最坏情况下均是O(nlgn)。
4、空间复杂度 需要一个辅助向量来暂存两有序子文件归并的结果,故其辅助空间复杂度为O(n),显然它不是就地排序。 注意: 若用单链表做存储结构,很容易给出就地的归并排序。
5、比较操作的次数介于(nlogn) / 2和nlogn - n + 1。
6、赋值操作的次数是(2nlogn)。归并算法的空间复杂度为:0 (n)
7、归并排序比较占用内存,但却是一种效率高且稳定的算法。
六、代码实现
public class MergeSortTest { public static void main(String[] args) { int[] data = new int[] { 2, 4, 7, 5, 8, 1, 3, 6 }; System.out.print("初始化:\t"); print(data); System.out.println(""); mergeSort(data, 0, data.length - 1); System.out.print("\n排序后: \t"); print(data); } public static void mergeSort(int[] data, int left, int right) { if (left >= right) return; //两路归并 // 找出中间索引 int center = (left + right) / 2; // 对左边数组进行递归 mergeSort(data, left, center); // 对右边数组进行递归 mergeSort(data, center + 1, right); // 合并 merge(data, left, center, center + 1, right); System.out.print("排序中:\t"); print(data); } /** * 将两个数组进行归并,归并前面2个数组已有序,归并后依然有序 * * @param data * 数组对象 * @param leftStart * 左数组的第一个元素的索引 * @param leftEnd * 左数组的最后一个元素的索引 * @param rightStart * 右数组第一个元素的索引 * @param rightEnd * 右数组最后一个元素的索引 */ public static void merge(int[] data, int leftStart, int leftEnd, int rightStart, int rightEnd) { int i = leftStart; int j = rightStart; int k = 0; // 临时数组 int[] temp = new int[rightEnd - leftStart + 1]; //创建一个临时的数组来存放临时排序的数组 // 确认分割后的两段数组是否都取到了最后一个元素 while (i <= leftEnd && j <= rightEnd) { // 从两个数组中取出最小的放入临时数组 if (data[i] > data[j]) { temp[k++] = data[j++]; } else { temp[k++] = data[i++]; } } // 剩余部分依次放入临时数组(实际上两个while只会执行其中一个) while (i <= leftEnd) { temp[k++] = data[i++]; } while (j <= rightEnd) { temp[k++] = data[j++]; } k = leftStart; // 将临时数组中的内容拷贝回原数组中 // (原left-right范围的内容被复制回原数组) for (int element : temp) { data[k++] = element; } } public static void print(int[] data) { for (int i = 0; i < data.length; i++) { System.out.print(data[i] + "\t"); } System.out.println(); }} 七、运行结果 初始化: 2 4 7 5 8 1 3 6 排序中: 2 4 7 5 8 1 3 6 排序中: 2 4 5 7 8 1 3 6 排序中: 2 4 5 7 8 1 3 6 排序中: 2 4 5 7 1 8 3 6 排序中: 2 4 5 7 1 8 3 6 排序中: 2 4 5 7 1 3 6 8 排序中: 1 2 3 4 5 6 7 8 排序后: 1 2 3 4 5 6 7 8
==================================================================================================
作者:欧阳鹏 欢迎转载,与人分享是进步的源泉!
转载请保留原文地址:
==================================================================================================
